Note: the images in this page are a bit out of date; they refer to Burnable Payments as "BOPs" and don't necessarily resemble the latest version of the Toastycoin interface.
Aside from these superficial discrepancies, the information below remains accurate.
Rules of the Game
First, let's go over some relevant rules of the Burnable Payment "game".
- A payer creates a BP with a certain amount of ether, a service request (in the title and initial statement), and with a specified service deposit.
- None of the settings of the BP can be changed after creation (although the payer can add additional statements or deposit more funds).
- Any Ethereum user can become a worker by matching the service deposit required to engage the BP. The BP then enters the Committed state, in which:
- The payer can no longer recover the ether in the payment.
- The worker is "locked in" to the BP (this role can never be changed or revoked).
- The payer can release the payment to the worker, or burn (meaning destroy) it.
There are a few more aspects we will ignore for now and return to further below:
- The payer can release/burn the payment in parts, rather than at once.
- There is an additional "auto-release" feature that protects against lazy payers.
(We encourage Solidity developers to follow along in the source code.)
(Disclaimer: Below we will use the words "never" and "always". We use these terms when the reality is "close enough to count", like how one might say "the bathroom on the 4th floor is always crowded" or "you'll never hit a car at a traffic light if you only go when it's green." While not technically true, these statements are reliable enough to influence you to avoid the 4th floor bathroom or drive through a green light. Similarly, the below text will make "never" and "always" claims that are accurate enough for BPs to be useful.)
The Game Tree
In this discussion we'll make use of a couple tools from game theory: game trees and backward induction. If these concepts are new to you, I suggest taking a look at this introduction to game trees, which uses backward induction (but doesn't explicitly say so), as well as the wiki on backward induction.
First, we'll build our game tree. The first node is the beginning of our "game"&emdash;the creation of the BP by the payer. Each subsequent level represents a choice one of the players can make.

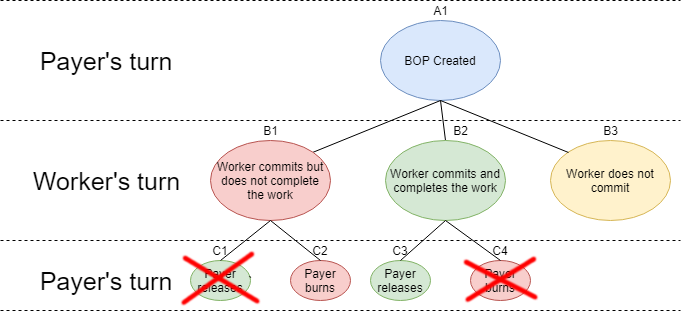
Each node with no children represents an end state to the game. Here we can see there are 5 end states:
- C1: The worker commits and fails to complete the work, and the payer releases the payment.
- C2: The worker commits and fails to complete the work, and the payer burns the payment.
- C3: The worker commits and completes the work, and the payer releases the payment.
- C4: The worker commits and completes the work, and the payer burns the payment.
- B3: The worker never commits in the first place.
Using backward induction, we will begin at the bottom row of the game tree: row C. This row represents the payer's choice in each case, so we'll view things from his perspective.
His choice:
To Burn or Release
First, a couple notes:
- We assume the payer intends to possibly use BPs in the future, and is therefore mindful of the reputation he builds and how it impacts his future success with BPs. We will revisit this assumption further below.
- Regardless of the payer's decision, he will not recover the ether in the payment, so it does not figure into the payer's choice on turn C.
- Whether the work is provided or not has been decided in the previous turn; therefore this will not impact the payer's decision: either he has the product or he does not, and his choice here will not change that.
- We ignore emotional responses like gratitude or anger. Although they would strengthen the argument for BPs, they don't really have a place in game theoretical analysis.
In this outcome, the payer will establish a reputation for releasing a payment even if the worker does not complete the task. With such a reputation, lazy, incapable, or dishonest workers will be more likely to commit to the payer's future BPs. "After all," they might think, "he's released the payment for no work before; perhaps he'll do it again." Such a reputation would thereby decrease the future utility of BPs&emdash;we could say that the payer has been marked as an "easy target".
This is a negative outcome, to the extent that the payer expects to try to use the service again, because he will face a greater risk of attracting scammers or lazy/incompetent workers.
C2: No work delivered; payer burns paymentHere, the payer establishes a reputation for burning the payment in response to a worker who does not complete the work. This will have an opposite effect of outcome 1: lazy, incapable, or dishonest workers will be less likely to commit to the payer's future BPs. "It didn't work the first time; it's unlikely to work next time." This would increase the future utility of BPs by dissuading such attempts.
C3: Work delivered; payer releases paymentHere the payer establishes a reputation for releasing the payment in response to completed work. Like choice C1, this makes it more likely that a worker will commit, but unlike C1, it's only confident, honest workers that will be thus attracted. "He released for good work last time; therefore, it's likely he'll release again if I can do the work."
This increases the future utility of the BP mechanism for the payer.
C4: Work delivered; payer burns paymentLike outcome 2, this makes others less likely to commit, but this time it's dissuading even honest, capable workers. This decreases the utility of future BPs.
Concluding Turn C
A rational payer will never choose options C1 or C4. With the payment already spent, and the work already either delivered or not delivered, the payer will choose to build a reputation that makes any of his future BPs more successful.
In short, he will always choose to release for completed work, and burn otherwise.
This might seem like an underwhelming conclusion for so much work, but we now know what a rational payer will do in every single case, and can cross off certain outcomes as game theoretically impossible.
We can now move up a level, to row B.
To Scam, Work, or Not Commit at all.
At row B, the worker is looking at an Open BP and deciding whether to commit and, if so, whether to attempt to do the work. It's convenient at this point to define some variables:
- D: The service deposit, which the worker must pay if he chooses moves B1 or B2.
- P: The original payment amount, which the worker will get (along with a refund of D) if the payer releases the payment.
- E: The effort required of the worker to complete the work requested in the BP
We will assume the worker has modeled the payer as a rational actor. Let's see how each choice works out.
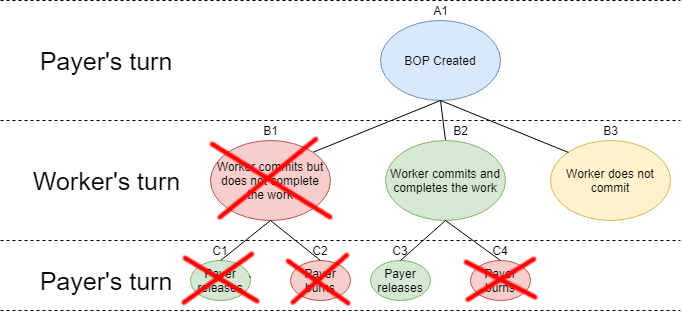
B1: Worker commits but does not do the workThe worker must pay D to make this choice, and we know that the payer will respond by burning the entire payment, arriving at outcome C2.
Endgame worker payout: (-D)
B2: Worker commits and does the workHere the worker still must pay D in addition to paying the "cost of effort" E for actually doing the service. But in the next turn, the payer will release the payment, which includes both the original payment P and the service deposit D. Since D is returned by endgame, we can ignore it:
Endgame worker payout: P - E
B3: Worker does not commitThis one's pretty simple: the worker pays no service deposit, doesn't make any effort, and doesn't receive a payment.
Endgame worker payout: 0
Concluding Turn B
We can make a couple conclusions from this.
- If the worker will not produce the work, he is better off not committing at all (payout: 0) than committing (payout: -D).
- If the worker can produce the work, and the cost of effort E is less than the payout P, he is better off committing (payout: P-E > 0) than not committing (payout: 0)
In no case is node B1 chosen, so we can cross it off, as well as its remaining child node.
With that, we can finally make an interesting statement about BPs.
Why create a BP?
When a payer creates a BP, anyone else considering committing will almost definitely make one of two choices:
- They don't commit, either because they don't intend to provide the service or because they don't expect the effort to be worth the payout.
- They do commit, indicating they do intend to provide the service and are confident they'll be able to. (The higher the service deposit, the more confident they must be.)
So, why would a payer open a BP? Because if no one commits, he can recover the payment, and if someone does commit, there is a strong game-theoretical guarantee that the worker will complete the work. The higher the service deposit, the stronger the guarantee.
Some Loose Ends
What if the payer doesn't intend to use the service again?
When analyzing row C of our game tree, we took into account the effect a choice would have on the payer's reputation. But if the payer is sure he'll never use BPs again, he won't care about his reputation. Indeed, he may not even bother to return to release or burn the payment, after the service is rendered. Why should he (other than to be nice)?
This is an issue because we can no longer logically assume the payer's final choice, row C, in our game tree, which means we can't analyze rows B or A either. To help alleviate this, BPs have an "auto-release" feature.
Auto-release is essentially protection for the worker against lazy payers, and has the following rules:
- The payer sets the auto-release time upon BP creation. This can be anywhere from a few minutes to several years.
- The timer begins to countdown as soon as a worker commits.
- The payer can reset the timer to the maximum as many times as he wants.
- If the timer runs out, the worker can trigger an auto-release of the payment. The payment will close and send all contained ether to the worker.
With these rules, if a payer never returns to the payment after a worker has committed, the payment will eventually release. A "lazy payer" would make our game tree look like this:
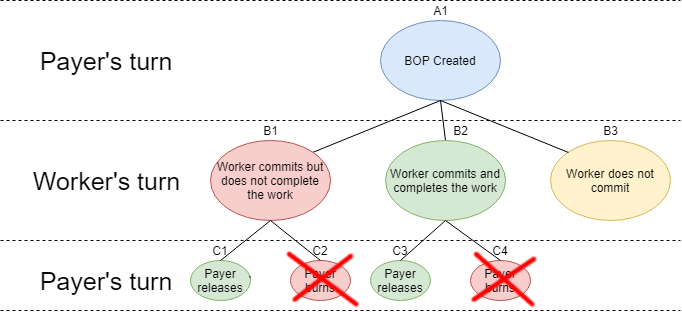
Of course, now we have another issue: a dishonest or incapable worker might now commit, counting on outcome C1. But this assumes that the worker somehow knows to model the payer as a "lazy payer." More likely, the worker will only suspect the payer might be lazy.
Even if a payer does not plan to use BPs again, he doesn't need to broadcast this information. Users looking at the open BP won't know whether to model the payer as a lazy payer who will never use BPs again, or a payer who is interested in building a good reputation. From the perspective of these users, we might draw our game tree like so:
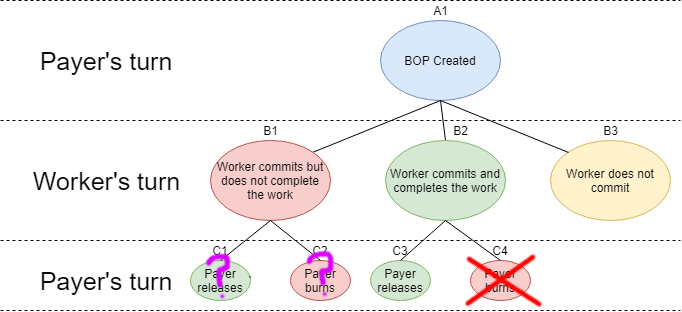
Here, we've combined the analysis of row C from our first assumption (the payer will make a choice with a mind to his reputation) with the lazy payment assumption (the payer will not return to the payment at all). In both scenarios, outcome C4 will never be chosen, so it's crossed out and outcome C3 is not. But whether outcome C1 or C2 is chosen depends on whether the payer is lazy.
Now honest workers still have a clear route to payment: whether the payer is lazy or not, they can guarantee a positive outcome by doing the work.
Dishonest workers hoping for outcome C1 must decide if the risk is worth it. A payer can dissuade this by increasing the service deposit and forcing the scammer to risk more, and in general convincing users that they will indeed be back to cast a final burn/release judgement.
Finally, this is really only an issue for a payer's very first BP. As soon as they have a reputation showing the right burn/release behavior, users viewing their BPs can count on this behavior continuing with a very high likelihood.
What if the worker provides bad or half-complete work?
We won't go into such rigorous analysis here, but we can still make some useful conclusions. What should a payer do, to maximize the utility of future BPs? Fortunately, a payer can choose to burn or release any part of the payment, giving him a more nuanced response than a binary punish/reward option.
For simplicity's sake, let's imagine the BP contains a request to mow the payer's lawn, and the worker does a bad job, leaving patches of tall grass.
Burning the whole payment would likely make future honest workers more reluctant to commit because they worry the payment might be burned if they're not "perfect". Releasing the whole payment isn't ideal either: this might be too much of a comfort, attracting workers who are not skilled and won't do a good job. A better response would be to burn part of it and release the rest, as well as log a payer statement explaining his reasoning (possibly including pictures of the issues). This way, future workers will know that mistakes will be punished, but not without mercy. Confident workers would still commit, but less confident workers will hesitate.
What about extortion attempts?
See the "No extortion attempts" section of this Medium article.
Don't some people just want to watch the world burn?
The concern here is that when a payer opens a BP, let's say with 3 ETH and a service deposit of 1 ETH, someone will spend 1 ETH to commit just to force the payer to burn the payment. As stated in this reddit comment, "So for 3 ETH I can force you to burn 15 ETH? Sounds like a good deal for me."
This only makes sense if someone both has money to spend, and has a really great time seeing a stranger's money go to waste on the Internet. Of course trolls abound on the Internet, but it's hard to imagine they'll be regularly shelling out real money just to confound someone's effort to spend money (although that might depend on what the payer is trying to buy).
In any case, to the extent that this is an issue, payers can just increase the service deposit amounts.